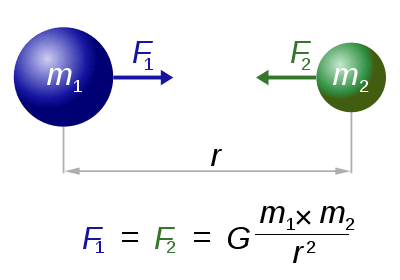
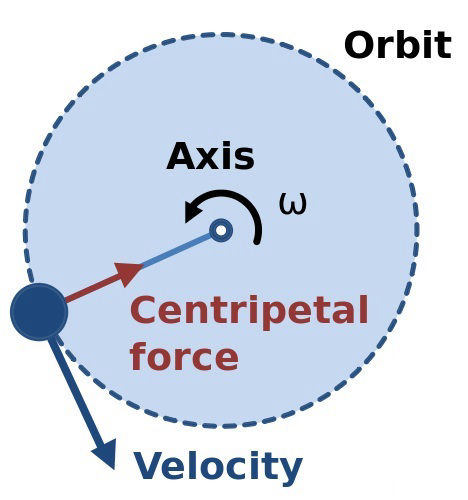
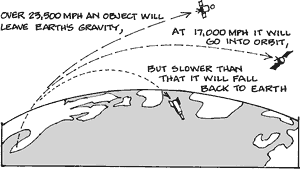
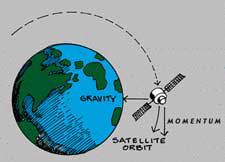
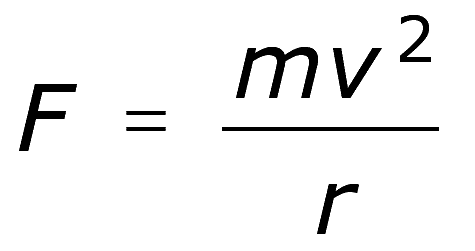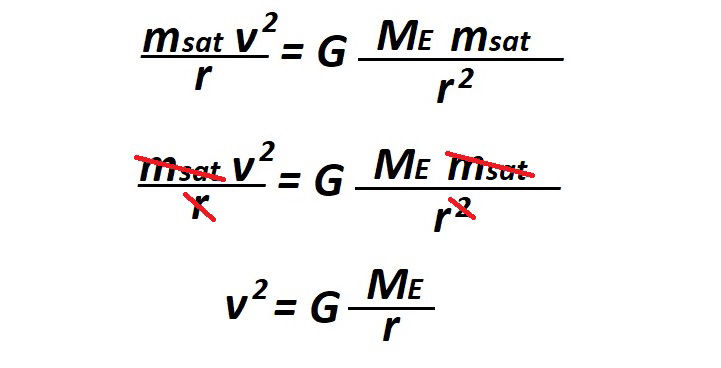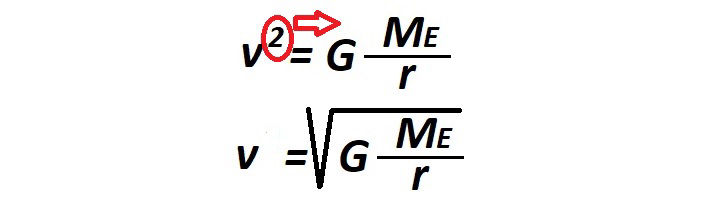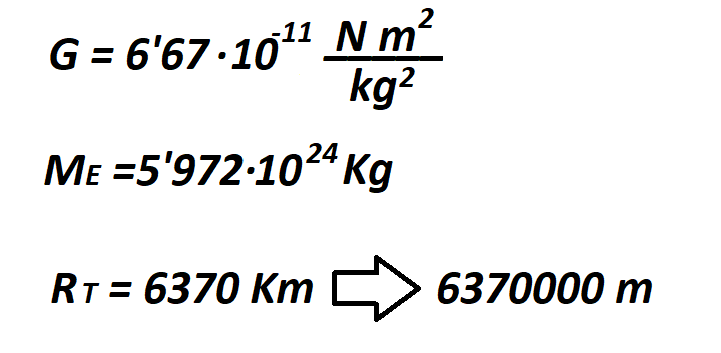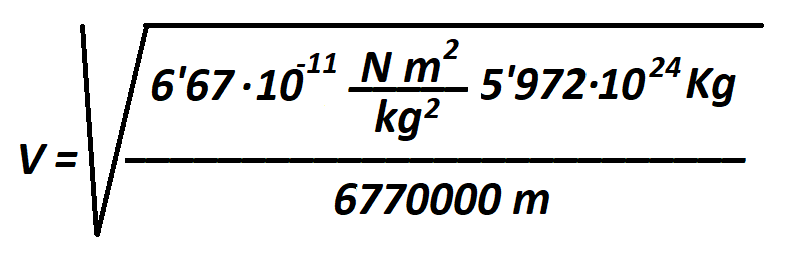ENG - Theory - Centripetal

Satellites and Orbits

May the Centripetal Force be with you...

Why Satellites don't fall down? Well, technically they fall down soon or later... let me explain...

Newton confirms that they must to fall back to Earth as the apple did on his head.

Newton's Law of Universal Gravitation

As Wikipedia says: Newton's law of universal gravitation states that a particle attracts every other particle in the universe with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.

where:
F is the force between the masses;

G is the gravitational constant (6.674×10−11 N · (m/kg)2);

m1 is the first mass (for example Earth)

m2 is the second mass (for example our Satellite)

r is the distance between the centres of mass.

Then... If every mass attracts every other mass with a force along the line intersecting both masses, why Satellites still stay up? Easy: it's because they are flying fast.

Then... If they are flying fast... Why they are not going far away and instead they are turning around the Earth?

Luckily there is another Force.

The centripetal Force:

The idea was to put again a copy paste of the Wikipedia's definition but believe me... it's not a good idea.
Let me try to explain what is the centripetal force. When you run normally you are moving straight foreward.
Now imagine that you run with a hand caught to a lamppost. What happens? you are running as before but a Force (your arm) does not let you get away from the pole. Your arm is the centripetal force. A Satellite is always falling to the Earth. But velocity tries to push it away. The sum of forces is a circular motion.

F is the Centripetal force
m is the mass of the satellite
v is velocity
r is radius. Remember: the distance from the satellite to the centre of the planet, not to the surface.

Of course, if velocity is too fast the satellite will leave Earth's gravity. If it is slower than requested the satellite fall back to Earth.

Surely you see that: Centripetal Force and Gravity are the same force... Yes

We are going to use the next formulas where : first formula Fc is Centripetal Force, msat is Satellite mass, v is velocity of the Satellite, r radius or distance between the centre of the satellite and the centre of Earth, the second one FG is Gravity Force, G is the gravitational formula, ME is the Earth mass, msat and r the same as said before.

That means:

At the moment we can see that Satellite mass is not critical. We continue..

Great! we have a formula to know the velocity of our Satellite. We can see the most important things are the mass of the planet to orbit and the distance between the centre of the planet and the satellite.

Now we are going to concentrate on Earth numbers, thanks again to Wikipedia. Remember to use the standard units (meters and kilograms, not Km or Tons, etc...)

Now we are going to use the ISS as an example. The ISS orbits normally arround 400 km high. That means R = RT + R iss = 6370 Km + 400 Km = 6770 Km

Knowing that Newtons(N) are mass(Kg) x Gravity(m/s2) we can finish the calculations:

BACK